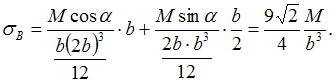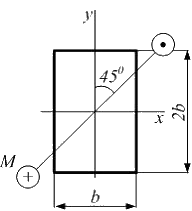
Поперечное сечение стержня прямоугольник с размерами b и 2b. Плоскость действия изгибающего момента М расположена над углом
к главным центральным осям. Значение максимального нормального напряжения в данном сечении равно …
- ✓
Раскладываем момент на составляющие относительно координатных осей x и y, тогда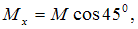 
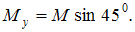
При косом изгибе нормальное напряжение в произвольной точке сечения определяется по формуле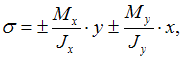
где x, y – координаты точки в системе главных центральных осей по абсолютной величине.
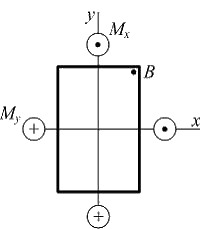
От изгибающего момента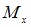
верхняя половина сечения работает на растяжение, нижняя – на сжатие. Момент 
вызывает растяжение правой половины сечения, сжатие – левой.
Следовательно, значение максимального нормального напряжения, которое возникает в точке В с координатами
равно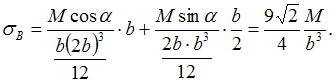 
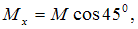
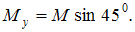
При косом изгибе нормальное напряжение в произвольной точке сечения определяется по формуле
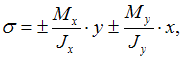
где x, y – координаты точки в системе главных центральных осей по абсолютной величине.
От изгибающего момента
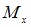верхняя половина сечения работает на растяжение, нижняя – на сжатие. Момент вызывает растяжение правой половины сечения, сжатие – левой.Следовательно, значение максимального нормального напряжения, которое возникает в точке В с координатами
равно 